本文详细解读 AlphaTensor,包括此工作在宏观上的定位意义和未来展望、在微观上的算法细节和结果,只需了解矩阵乘法即可阅读本文。有 RL (reinforcement learning 强化学习) 或 AutoML (自动机器学习) 基础会更好~ 一些参考链接:[blog] [github] [paper-abs] [paper-pdf] [paper-appendix].
这是原提问中笔者的一个简要回答:
如何看待DeepMind最新的AI系统AlphaTensor可以发现矩阵相乘的求解方法?283 赞同 · 27 评论回答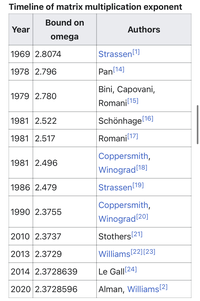
背景介绍:矩阵乘
矩阵是非常重要的数学工具,尤其对于深度学习。全连接层几乎处处都在矩阵乘,而卷积神经网络的现代实现 (cuda im2col + GEMM) 也非常依赖矩阵乘。已经有无数的工作在优化计算机的矩阵乘效率。system角度的优化就有向量化、访存命中等等。而从数学角度,矩阵乘需要的计算次数其实也有优化空间。
在一次矩阵乘中,包含了许多次对两个数字的数值乘法或加法运算。考虑计算机架构的乘指令开销远大于加法,我们希望在保证结果正确的前提下,尽量减少矩阵乘中的数值乘法次数。下图是一个 $2×2$ 矩阵乘的例子,请见图注。

对A、B两个2x2矩阵相乘得到C。左:按照矩阵乘法的定义需要做8次数值乘法 即h1~h8。右:按照Strassen在50年前提出的算法只需要7次。

一句话介绍 AlphaTensor
AlphaTensor利用人工智能技术 (RL强化学习) 对算法 (矩阵乘) 流程进行自动设计。
重点/难点在哪?搜索空间
可以看到上面"自动设计算法"这一套其实很像一个自动超参数优化问题:三要素 (搜索空间、搜索方法、优化目标) 非常明确。之前做自动机器学习AutoML/NAS的同学应该很熟悉这套方法论。而想套用这套方法论,难就难在第一步如何定义搜索空间,即如何把矩阵乘算法的流程进行数学化的抽象 (参数化)。
怎么定义搜索空间? 两个对应
AlphaTensor使用如下两个对应关系来构造搜索空间 (实际上这个搜索空间是已有的,在[2]中会看到这个搜索空间已被很多前人工作使用):
这样,通过自动尝试找更小的R,就可以"自动设计算法"。以 $2×2$ 矩阵乘为例,其表征张量[3]记为 $T2$,张量尺寸是 $4×4×4$,总共包含64个元素。请见下图与图注:
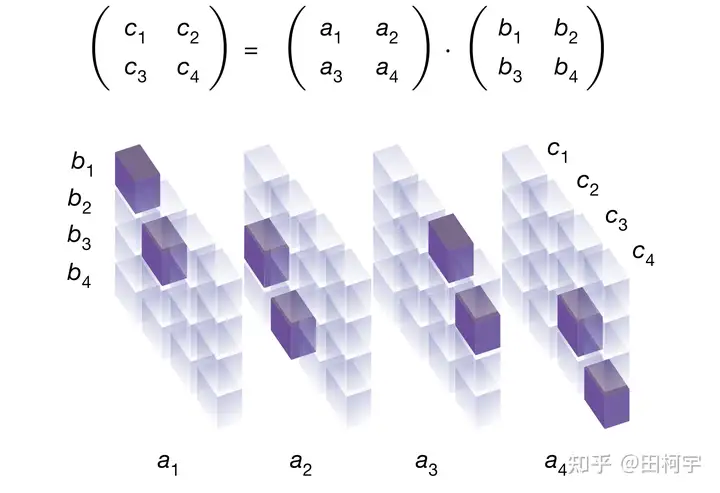
一个尺寸为4x4x4的矩阵乘法表征张量T2,其对应2x2矩阵的乘法定义即C=A·B;张量T2有4x4x4=64个元素,深色取值为1,浅色取值为0