论文研读报告 | MuZero算法:Model-based的里程碑
[TOC]

这篇文章的研究内容为:具有规划能力的智能体(agents with planning capabilities)。
在此之前,很多研究都是使用基于树的规划方法(Tree-based planning methods),然而在实际业务应用中,动态的控制/仿真环境,往往是复杂且未知的。
这篇文章提出了一个算法:MuZero,它通过将基于树的搜索(tree-based search)与学习模型(learned model)相结合,可以在不知道环境基本动态的情况下表现的很好。
这里的学习模型(learned model),这个模型实际上是在applied iteratively的时候,可以预测出与planning最相关的reward、action-selection policy以及value function。
因此,总结一下,MuZero的研究目的有两个:
- 一是如何在不知道状态转移规则的情况下使用蒙特卡洛树搜索算法
- 二是设计一个Model-based的算法在视觉信息丰富的环境(如Atari游戏)上表现优于Model-Free算法。
下面就开始看具体的工作了!
1 算法简介
1.1 背景
基于前瞻搜索(lookahead search)的规划算法,有很多的应用。然而这些规划算法都依赖于精确的模拟器和严谨的规则,不能直接用于现实领域。
我们知道,强化学习算法分为Model-based和Model-free。一般来说,我们的研究主要集中于Model-free的方法,即直接从与环境的交互作用中估计最优策略以及价值函数。这些方法在一些视频游戏,比如雅达利中表现的时候不错的。但是,model-free在需要精确和复杂的前瞻性(lookahead)的领域,比如围棋或国际象棋,效果就没有那么理想了。
而一般的Model-based的强化学习方法,Model实际上是一个概率分布,是构建真实的environment,或者是full observation。先从环境的dynamics中学出一个model,然后根据所学的model进行规划。但是在雅达利游戏实验中,表现的不如Model-based。
本篇文章,就是介绍了一种新的Model-based的强化学习方法MuZero,既能够在视觉复杂的雅达利上表现的很好,又能在精确规划任务中也表现的很好,
MuZero算法基于AlphaZero强大的搜索(powerful search)以及基于搜索的策略迭代(search-based policy)算法,并在训练过程中加入了一个学习模型(learned model)。
除此之外,MuZero还将AlphaZero扩展到更广泛的环境集,包括单智能体域(single agent domains)和中间时间步长(intermediate time-steps)的非零奖励(non-zero rewards)。
小总结:
Planning(规划算法)是一个比较难的研究点,我们熟知的AlphaGo是基于树的规划算法,但是这类算法需要一个完美的环境模型,这个条件在真实的世界中是很难被满足的。
DeepMind的MuZero算法是model-based RL的里程碑式成果,是推动强化学习解决真实世界中的问题的新一步进展。
1.2 理解算法思想
首先,我们开宗明义地介绍一下MuZero算法的思想:
MuZero算法的主要思想,是构造一个抽象的MDP模型,在这个MDP模型上,去预测与Planning直接相关的未来数据(策略、价值函数以及奖励),并在此基础上预测数据进行规划。
那么为什么要这样做,以及这样做为什么是有效的呢?下面就把论文中的内容“掰开”“揉碎”,理解算法的思想:
1.2.1 为什么要抽象
我们知道,大多数Model-Based强化学习方法,都是学出一个与真实环境所对应的Dynamics Model。
然而,如果是为了做Planning,我们并不关心这个Dynamics Model是否准确地还原了真实环境。
我们只要这个Dynamics Model所给出的未来每一步的value和reward都接近真实环境中的值,那么就能作为Planning中的模拟器来使用。
MuZero算法,就是先将真实环境中获取的状态,通过一个编码器(representation function)转换成一个没有直接约束的抽象的状态空间(abstract state space)中的一个隐藏状态(hidden state,通过前一个隐藏状态和假设的下一个动作进行循环迭代)。
然后在这个抽象的状态空间中,去学习Dynamics Model和value prediction,对每一个隐藏状态上的策略都进行预测(这就是与<Value prediction network>这篇论文不同之处),得到Policy Prediction Network。
然后,使用蒙特卡洛树搜索,将Dynamics Model当作模拟器,在抽象的状态空间中做Planning,预测接下来若干步的策略、价值函数以及奖励。
这里的隐藏状态,并不是要拟合真实环境。而是令在抽象状态空间中训练的Dynamics Model以及价值预测网络,可以在初始的隐藏状态以及执行未来k步后,对未来k步的value和reward的预测,与真实环境中通过搜索的value以及观察到的reward尽可能的相近。
简单讲,就是在虚拟状态空间中先学出一个环境模型,然后再基于这个所学到的环境模型,在无法与真实环境交互过多的情况下进行规划。
1.2.2 为什么有效
那么我们如何保证抽象MDP中的planning与真实环境中的planning等价呢?
这种等价是通过确保价值等价(value equivalence)来实现的。
即从相同的真实状态开始,通过抽象MDP的轨迹的累积报酬与真实环境中轨迹的累积报酬相匹配。
2 模型图文讲解
首先,总体数据一下模型的数学表达:
给定一个隐藏状态 s^{k-1} 和一个候选动作 a^k ,动态模型g需要产生一个即时奖励r^k和一个新的隐藏状态g。策略p^k和值函数v^k由预测函数f通过输入s^k计算得到v^k=f_\theta(s^k)。动作a_{t+1}从搜索策略\pi_t中采样得到。环境接收到一个动作生成一个新的观测o_{t+1}和奖励u_{t+1}。
下面,通过图文结合的方式,具体说一下如何通过learned model进行Planning、acting、以及training。
2.1 MuZero中模型的组成
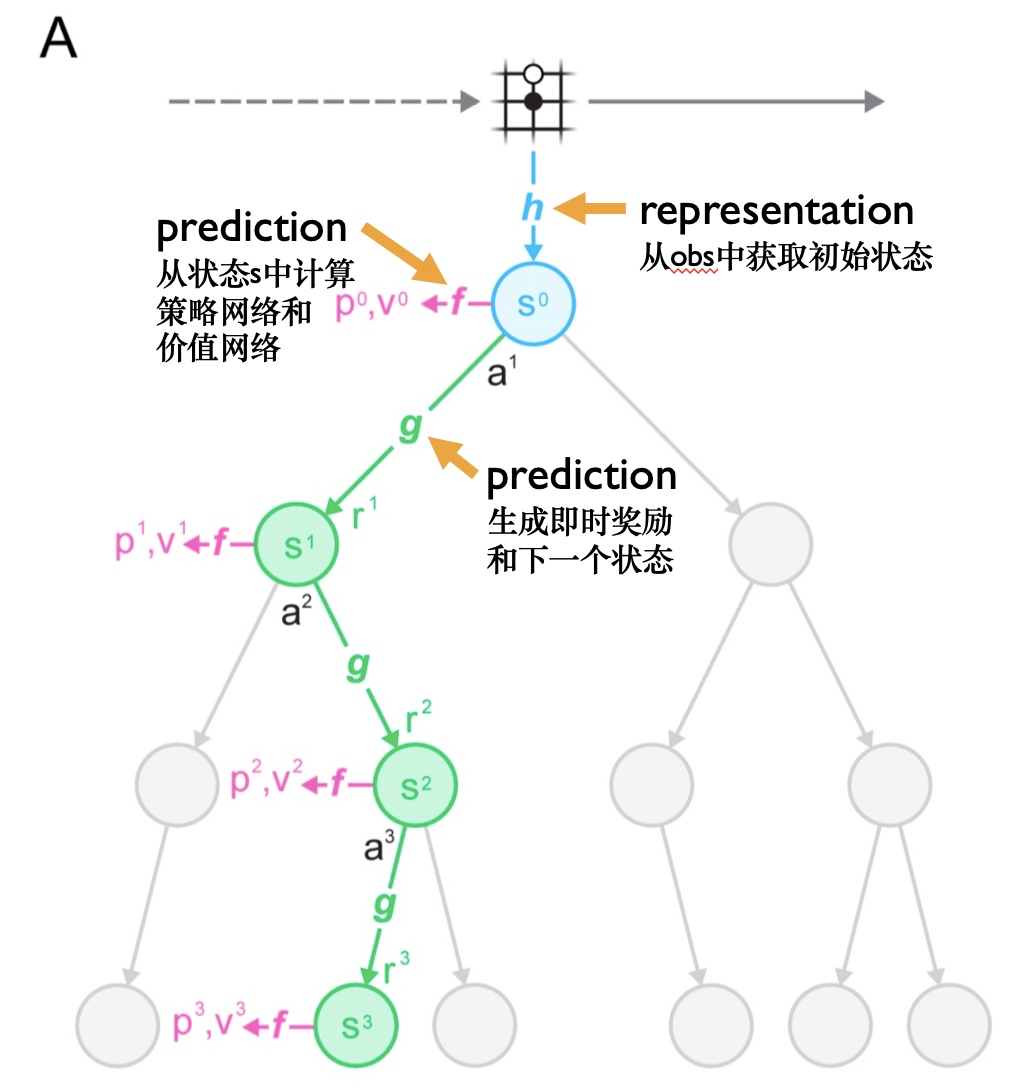
MuZero是如何使用模型进行规划的呢?我们来看A图:
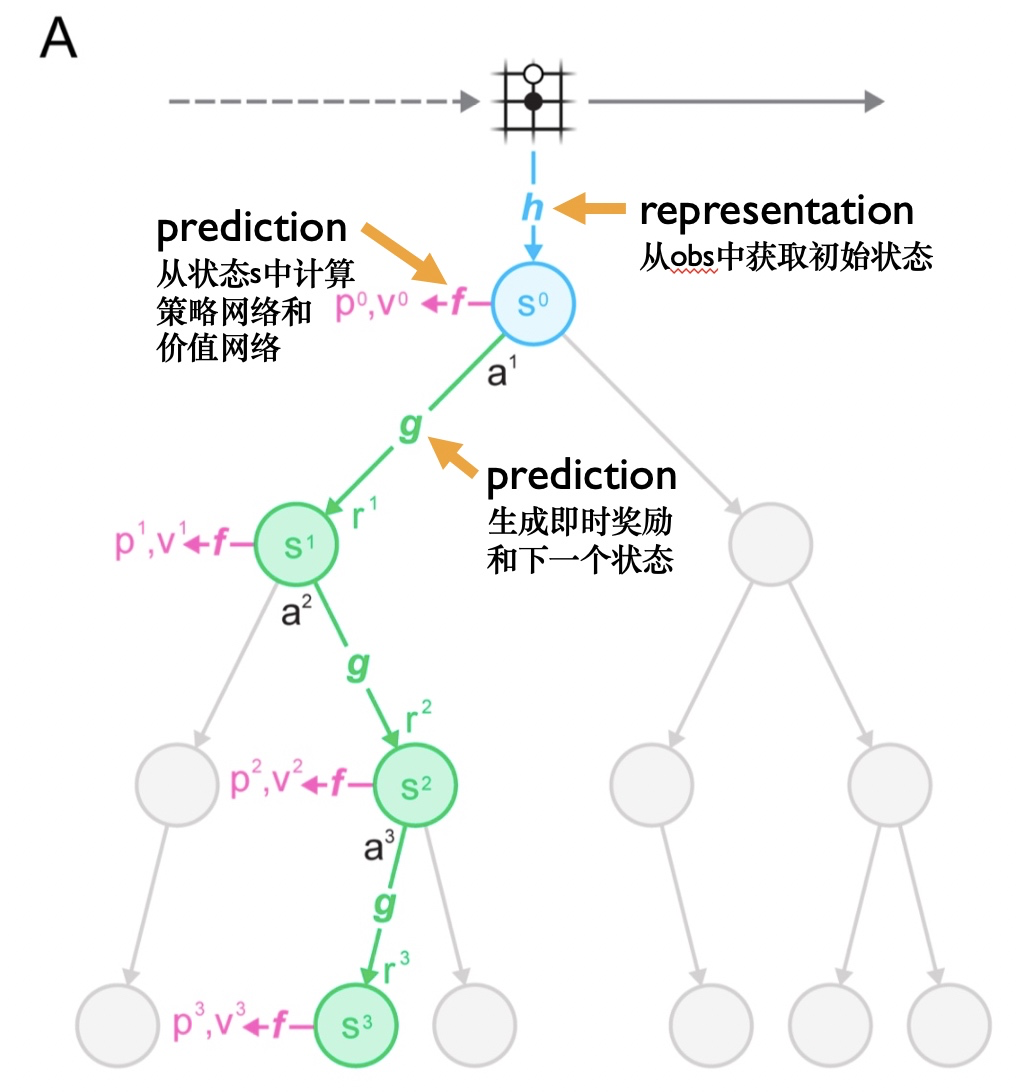
所谓的模型,由以下3个相互连接的部分组成:
representation:表征编码器h: s^0 = h(o_1,...,o_t),从历史观测,转换为初始状态。在上面的树型模型中,将连续的t帧观测\{o_1,...,o_t\}传给`representation函数h中获得初始隐藏状态s_0。
dynamics:生成器g: r^k, s^k = g(s^{k-1}, a^k),表示系统中的动态变化。给定前一个隐藏状态(previous hidden state)s_{k−1}和一个候选操作a^k,dynamics函数$g$就会产生一个即时奖励(immediate reward)r^k和一个新的隐藏状态s^k。
prediction:预测器f: p^k, v^k = f(s^k)。策略p^k以及价值函数v^k是通过prediction函数$f$ 从隐藏状态$sk$中计算出来的。
2.2 MuZero如何与环境进行交互并决策
图A中所描述的是:在每一个step中,隐藏状态执行一次蒙特卡洛树搜索的到下一个动作。
那么MuZero如何在环境中进行决策呢?
下图是横向的看每一步棋的态势:
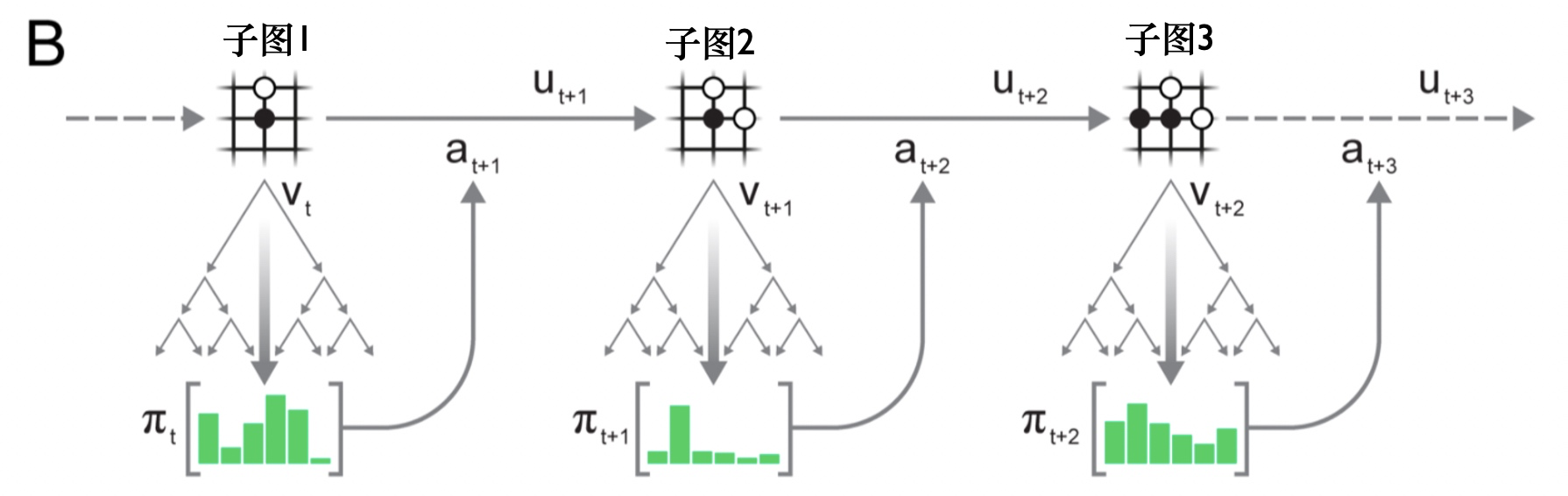
对于子图1(一黑一白)中所描述的态势而言,使用蒙特卡洛树搜索对其进行建模,得到一个策略网络$\pi_t$,并针对策略网络进行采样,选出可执行动作$a_{t+1}$,这个动作,是与MCTS根结点的每个操作的访问计数成正比的。
在执行动作a_{t+1}之后,得到奖励u_{t+1},得到下一时刻的观测(子图2),同样的使用MCTS进行建模,得到策略网络\pi_{t+1},并选出可执行动作a_{t+2}。
环境接受了行动,产生了一个新的观察$o{t+2}$和回报$u{t+2}$,得到子图3。
就这样不断往下推演,在episode结束时,轨迹数据被存储到回放缓冲区(replay buffer)中。这就得到了一个决策。
2.3 MuZero如何训练模型
那么MuZero是如何训练模型的呢?我们看下图的过程:
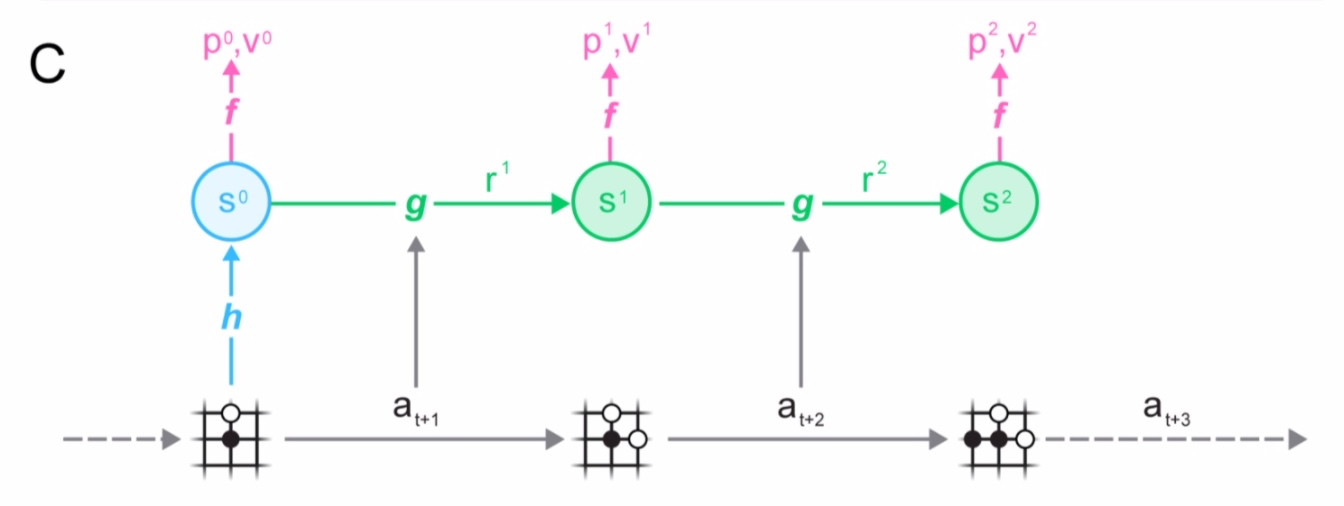
对Replay Buffer中的轨迹数据进行采样,选取一个序列,然后根据该轨迹运行MuZero模型。
在初始的step中,编码器representation function $h$接受来自所选轨迹(the selected trajectory)的过去观测值o_1,...,o_t。
随后,模型展开K步循环。
在第k个步骤中,生成器dynamics function g接收上一步的隐藏状态s^{k-1}和真实的动作a_{t+1}。
编码器representation function、生成器dynamics function以及预测器prediction function的参数,通过时间回溯(backpropagation-through-time)进行端到端的联合训练(jointly trained),则可以预测三个量:
- 策略网络:p^k \approx \pi_{t+k}
- 价值网络:v^k \approx z_{t+k}
- 即时奖励:r^k \approx u_{t+k}
其中$z_{t+k}$是一个采样的返回(a sample return),比如棋类游戏中的最终奖励,或者Atari中n步的奖励。
3 MuZero算法详解
3.1 价值网络和策略网络
MuZero是一种机器学习算法,因此自然要先了解它是如何使用神经网络的。
简单来说,该算法使用了AlphaGo和AlphaZero的策略网络和值网络:
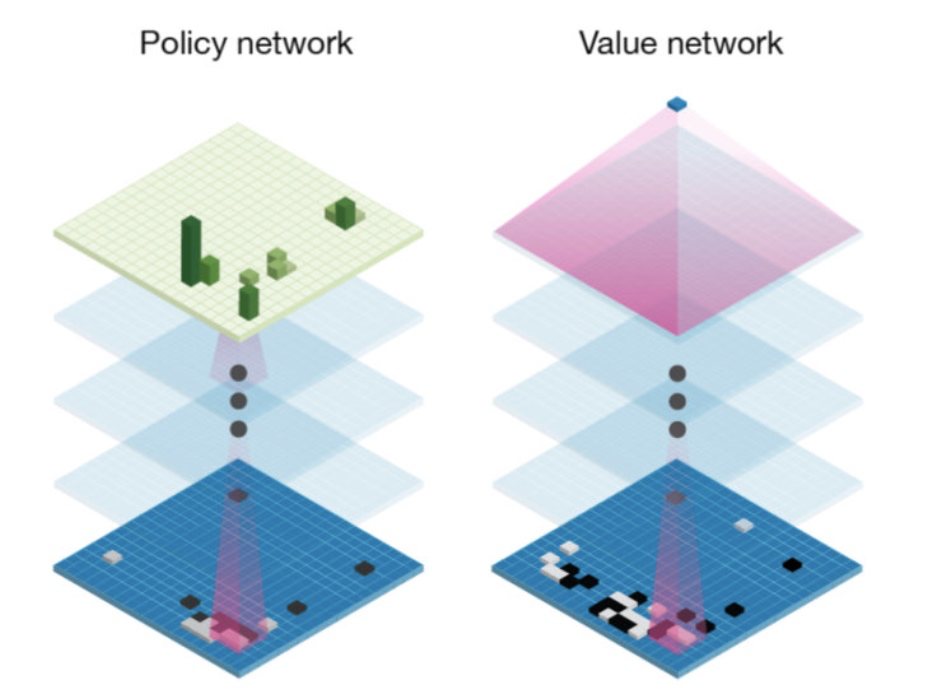
策略网络和价值网络的直观含义如下:
- 策略$p(s,a)$表示在状态$s$时所有可能的动作$a$分布,据此可以估计最优的动作。比如,在下棋的时候,玩家会想我当前可能会如何走,对手如何走,我怎么走是最优的。
- 价值$v(s)$是对当前状态$s$下获胜的可能性的评估,即通过对所有的未来可能性进行加权平均,确定当前局势的获胜概率。
根据策略网络,能够预测每一步的动作;依赖价值网络,可以选择价值最高的动作。将这两个估计结合起来可以得到更好的结果。
3.2 MuZero中的蒙特卡洛树搜索
3.2.1 简单介绍MCTS
MuZero也是使用MCTS(蒙特卡洛树搜索)来汇总神经网络,来在当前环境中,去预测并选择下一步动作的。当到达结束后,树中的每一个节点都会存储一些相关参数,包括被访问的次数,轮次,上一步动作的概率,子节点以及是否有所对应的隐藏状态和奖励。
蒙特卡洛树搜索,是一个迭代的,最佳优先(best-first)树搜索过程。其目标是帮我们计算出到底应该采用什么样的动作,可以实现长期受益最大化。
最佳优先,意味着搜索树的扩展(expansion)是依赖于搜索树中的价值评估(value estimates)。
与常见的深度优先、广度优先相比,最佳优先搜索,可以利用深度神经网络这种启发式估计,在非常大的搜索空间中寻找最优的解决方案。
蒙特卡洛树搜索具有四个主要阶段:
通过重复执行这些阶段,MCTS每次都会在一个节点的在未来可能的动作序列(action sequences)上逐步构建一棵搜索树。在这个树中,每一个节点都表示一个未来状态,而节点之间的连线则表示从一个状态到下一个状态的动作。
3.2.2 MuZero算法中MCTS的四个阶段
下面我们对应MuZero算法中的蒙特卡洛树搜索,看看以上四个阶段对应的是什么内容:
首先来看模拟。
模拟的过程类似蒙特卡洛方法,快速推演。为了得到某一个状态的初始评分,让游戏随机进行直到结束,记录模拟次数以及胜利次数。
接下来是选择。
虽然Muzero不知道游戏规则,但是它知道哪一步是可以走的。在每个节点(状态s),使用评分函数$UCB$比较不同的动作$a$,并选择评分最高的最优动作。
这里简单介绍一下UCB(Upper Conference Bound)策略,这是一种动作选择策略,主要用来解决\epsilongreedy在选择时的低效率问题。举个例子,\epsilon-greedy策略可以找到最好吃的那家餐厅,UCB则可以选出最喜欢吃的三家餐厅,并粗略的排个序。UCB的坏处是当数据量较小时,这个排序并非是与真实期望情况严格相符的排序,只是估计而已。也就是说UCB长于exploration,短于exploitation。UCB公式如下:
UCT(v_i,v)=\frac{Q(v_i)}{N(v_i)} + c \sqrt{\frac{log(N(v))}{N(v_i)}}
其中,Q(v)是该节点赢的次数,N(v)是该节点模拟的次数,$c$是常数。通过UCB公式,随着访问次数的增加,加号后面的值越来越小,因此我们的选择会更加倾向于选择那些还没怎么被统计过的节点,避免了我们刚刚说的蒙特卡洛树搜索会碰到的陷阱——一开始走了歪路。
回到MCTS问题上来。
每次模拟从s^0开始,终止于叶子结点s^l。对于模拟的每个step k=1,...,l,根据内部状态s^{k-1}最大化置信区间上界(UCB)选择最佳动作:
a^k = \arg \max_a [Q(s,a) + P(s,a) \centerdot \frac {\sqrt{\sum_b N(s,b)}}{1+N(s,a)}(c_1 + \frac {\sum_b N(s,b)+c_2+1} {c2})]
每选择一个动作,我们都会增加其相关的访问计数N(s,a),以用于UCB比例因子c以及之后的动作选择。
模拟沿着树向下进行,直到尚未扩展的叶子。此时,应用神经网络评估节点,并将评估结果(优先级和值估计)存储在节点中。
然后是扩展。
在选择了一个动作A之后,在搜索树中生成一个新的节点,对应上一个状态在执行完动作A之后的局面。
最后是回溯。
在模拟结束后,从子节点开始,沿着刚刚向下的路径往回走,沿途更新各个父节点的统计信息。每个节点都在其下保存所有值估计的连续均值,这使得UCB公式可以随着时间的推移做出越来越准确的决策,从而确保MCTS收敛到最优动作。
3.2.3 中间奖励
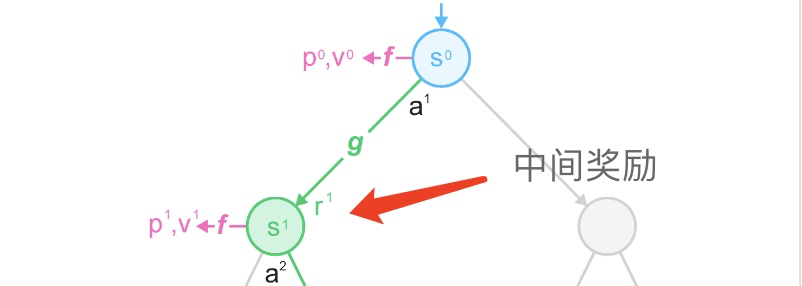
实际上,在MCTS的过程中,还包括对中间奖励r的预测。
在某些情况下,游戏完全结束后需要提供胜负反馈,这就就可以通过价值估计进行建模。但是在存在频繁反馈的情况下,每一次从一种状态转换到另一种状态后,都会得到回报r。
因此通过神经网络预测直接对reward进行建模,并将其用于搜索。在UCB策略中引入中间奖励:
U(s,a) = r(s,a) + \gamma \centerdot v(s') + c \centerdot p(s,a)
其中,r(s,a)是指在状态s时执行动作a后观察到的奖励,而折扣因子\gamma是指对未来奖励的关注程度。
由于在一些环境中,奖励是无界的,因此可以将奖励以及价值估计标准化到[0,1]期间,然后再与先验知识相结合:
U(s,a)=\frac{r(s,a)+\gamma \centerdot v(s')-q_{min}}{q_{max}-q_{min}} + c \centerdot p(s,a)
其中,q_{max}和q_{min}分别是整个搜索树中观察到的最大和最小r(s,a)+\gamma \centerdot v(s')估计。
3.3 整体描述
基于过去的观测值以及未来的行为a_{t+1},...,a_{t+k},对于给定的k=1...k步中的每一个step,通过一个带有参数\theta的模型\mu_\theta,在每个时间步$t$进行预测。
模型预测了3个量:
- 策略网络:p^k_t \approx \pi(a_{t+k+1}|o_1,...,o_t,a_{t+1},...,a_{t+k})
- 价值函数:v^k_t \approx E[u_{t+k+1}+\gamma u_{t+k+2}+...|o_1,a_{t+1},...,a_{t+k}]
- 即时奖励:r_k^t \approx u_{t+k}
其中u是真实地观测奖励,\pi是策略,\pi是折扣因子。
说白了就是拿到过去的观测数据,编码到当前的隐藏状态,然后再给定未来的动作,就可以在隐藏状态空间中进行规划了。
3.4 步骤分解
在每一个step中,模型由representation function、dynamics function以及prediction function组成:
dynamics function是生成器,其数学表示为:r^k, s^k = g_\theta(s^{k-1}, a^k)。它的反应了真实的MDP模型的结构,输出即时奖励以及状态的转换。其中,状态s^k,实际上只是隐藏状态,并没有拟合真实的环境模型,其目的是预测相关的未来的policy、values以及reward。并且在论文中g只是一个确定的函数,没有像其他强化学习方法加入随机性(后续工作可能会加入)
prediction function 类似于AlphaZero联合策略和价值的神经网络,可以从隐藏状态s^k计算policy和value function:p^k, v^k = f_\theta(s^k)。
representation function,对初始化根节点状态$s0$进行编码:s^0=h_\theta(o_1,...,o_t)。
通过这样的模型,就可以基于过去的观察o_1,...,o_t,在虚拟的未来轨迹a^1,...,a^k上进行搜索。
例如,可以简单地选择k步动作序列进行搜索,使值函数最大化。
也可以使用类似于AlphaZero搜索的MCTS算法,得到策略p^k和估计价值v^k,之后就可以从策略p^k中选择动作a^{t+1}。进一步的,执行该动作并生成中间奖励和状态空间。
在第k个step中,通过对模型的所有参数进行联合训练,使policy、value、reward与实际观察到的目标值像匹配。
对模型的所有参数进行联合训练,使每个假设步骤k的策略、价值和奖励与k个实际时间步骤过后观察到的相应目标值精确匹配。
通过MCTS,可以得到三个改进的策略目标(improved policy targets):
目标一:与AlphaZero类似,改进的策略目标是通过MCTS搜索生成的;第一个目标是最小化预测策略p^k_t和MCTS得到的搜索策略\pi_{t+k}之间的误差:l^p(\pi_{t+k}, p^k_t)。
目标二:在MuZero算法中,value的计算与AlphaZero中MCTS使用完整序列平均动作价值不同。MuZero中MCTS使用带衰减因子和中间奖励的长episode更新value,相当于使用了TD(n),速度更快、方差更小。公式为:z_t=u_{t+1}+\gamma u_{t+2} + ... + \gamma ^{n-1}u_{t+n} + \gamma^n v_{t+n}。其中u表示观测奖励、v表示累计价值。之后就可以最小化预测价值v^k_t和MCTS得到的z_{t+k}之间的误差:l^v(z_{t+k}, v^k_t)
目标三:最小化预测奖励r^k_t和观察到的奖励u_{t+k}之间的误差:l^r(u_{t+k}, r^k_t)
最后,添加L2正则化项,得到最终的损失函数:
l_t(\theta) = \sum_{k=0}^K l^r(u_{t+k}, r^k_t) + l^v(z_{t+k}, v^k_t) + l^p(\pi_{t+k}, p^k_t) + c||\theta||^2
4 总结
强化学习分为Model-based和Model-free两大类。
其中,Model-based强化学习方法需要构造环境模型。一般来说,环境模型是由马尔可夫决策过程(MDP)表示的。该过程由两部分组成:
- 状态转换模型(state transition model),用于预测下一个状态;
- 奖励模型(reward model),用于预测该转换期间的预期奖励。
模型一般是通过所选择的动作,或者临时抽象的行为进行训练。一旦建立了一个模型,就可以直接应用MDP规划算法(比如:值迭代value iteration、蒙特卡洛树搜索MCTS)来计算MDP的最优值或最优策略。
因此,在复杂环境或者部分观测的情况下,去构造模型应该预测的状态表示就很困难了。因为Agent没有办法去优化“the purpose of effective planning”的representation和model,这就导致了,representation learning、model learning以及planning之间就会出现分离。
而MuZero是一种完全不同的Model-based的强化学习方法,其重点是端到端预测值函数。主要思想是构造一个抽象的MDP模型,使抽象MDP中的规划等价于真实环境中的规划。
这种等价是通过保证价值等价来实现的,即从同一真实状态开始,通过抽象MDP的轨迹的累积报酬与真实环境中轨迹的累积报酬相匹配。
预测器$f$首先引入了价值等价模型(value equivalent models)在没有动作的情况下去预测value。
虽然底层的模型是MDP,但是它的转换模型不需要与环境中的真实状态相匹配,只要将MDP模型看作深度神经网络中的一个hidden layer就行。对展开的MDP进行训练,例如通过时间差分学习,使期望的累积奖励总和与实际环境的期望值相匹配。
然后,价值等价模型(value equivalent model)扩展到有行动优化价值中。TreeQN学习一个抽象的MDP模型,使得在该模型上的树搜索(由树结构的神经网络表示)逼近最优值函数。值迭代网络(value iteration networks)学习一个局部MDP模型,使得该模型上的值迭代(由卷积神经网络表示)逼近最优值函数。
价值预测网络(value prediction networks)比较接近MuZero:学习一个基于实际行动的MDP模型;展开的MDP经过训练,使得奖励的累积总和,以简单的前瞻性搜索产生的实际行动顺序为条件,与真实环境相匹配。没有策略预测,搜索只使用值预测。
通过对论文的学习,虽然理解了MuZero算法的思想,但是如果想要在实际项目中使用MuZero还是有不小的困难。
比如如何设计representation、dynamic以及prediction等等,这些都需要在对代码实现非常熟悉的情况下,再结合具体业务场景进行实现。
提供一个基于pytorch的muzero算法实现:https://github.com/werner-duvaud/muzero-general
如果有时间,还会继续研究代码,争取对论文进行复现。